Window, North Gate, Imperial Citadel of Thăng Long, Hanoi, Vietnam https://en.wikipedia.org/wiki/Imperial_Citadel_of_Th%C4%83ng_Long#North_Gate_(C%E1%BB%ADa_B%E1%BA%AFc,_or_B%E1%BA%AFc_M%C3%B4n)
#Tiling #TilingTuesday #Pattern #Geometry #MathArt #MathsArt #photography #architecture
#tiling
I'm wondering: #physics makes a lot of use of #periodic functions, in particular it is very useful to solve space-dependent equations in representative volumes with #periodicBoundaryConditions.
However I've only seen it done with periodicity along orthogonal directions, aligned with a Cartesian frame.
Do you know of work, e.g. #PDE resolution, in nonrectangular #periodicDomains? E.g., in a #tiled hexagon? (but with a sufficiently generic setting, not exploiting regular hexagon symmetries) Even better if the periodicity parameters themselves are among the unknowns.
(Maybe I'm completely missing something obvious there, I'm in my first steps towards defining what I want - any random thought on the topic highly welcome!)
#tiling people?
Diagonal section of ðe 4d cartesian product of 2 "I want to be a sea urchin and eat cabbage"(yes, really) tilings
kinda like ðis
Unfortunately we are still too dimensionally, perceptually, & probably intellectually challenged to even try to look at ðe full θing
Two tilings of tangent circles for #TilingTuesday .
#MathArt #tiling #Mathematics
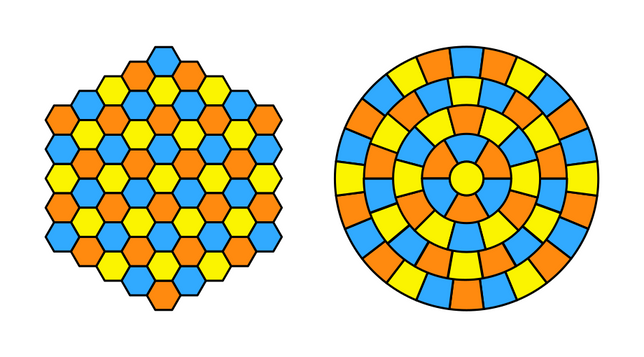
These two art pieces are based on the deformation of a hexagonal tiling into a topologically equivalent "tiling" composed of parts of concentric circles, all parts having the same area (third image). Selecting one hexagon as the center, we transform it into a circle of radius 1. Next concentric circle will hold the 6 adjacent tiles as sectors of rings. And so on, the circle of level n will have radius sqrt(1+3·n·(n+1)) (difference of radius when n tends to infinity approaches sqrt(3)). This map can be coloured with three colours, like the hexagonal tiling. For the artwork, suppose each sector of ring is in fact a sector of a circle hidden by inner pieces. Then choose a colour and delete all pieces not of this colour. Two distinct set of sectors can be produced, one choosing the central colour, one choosing another colour. Finally recolour the pieces according to its size.
#MathArt #Art #Mathematics #geometry #tiling
And for #TilingTuesday this simple #tiling with ellipse arcs.
#MathArt #Mathematics
Rhombicosidodecahedron
Face to face tiling 240 equilateral polyhedra.
Love this beautiful Art Nouveau style tenement tile pattern, featuring Scottish Bluebells. It's from a tenement close in the Pollokshields area of Glasgow.
Sierpinski Pyramid Tiling for #TilingTuesday
This kind of pyramid is a quarter of a cube.
'དཔལ་བེའུ།*16
(I'm like 90% sure ðe orange bit forms a single loop)